目次
大学・高校受験の数学の問題を、中学受験の算数の技で解く!
中学受験算数で学習するテクニックの1つとして、「天秤法(天秤算)」というものがあります。
こちらを利用することで、学生が一度は苦しむであろう難問を解くことができるようになるのです。
大学受験であれば「チェバの定理」や「メネラウスの定理」を用いる問題です。
高校受験であれば「食塩濃度」に関する問題です。
「公式が長くてややこしい…」
「条件整理が面倒でこんがらがってしまう…」
そんな日々におさらばしてしまいましょう!
天秤法の基本2パターン
まずは中学受験算数で学習する天秤法を理解する必要があります。
Point:天秤法
「左右のうでの長さの比」と「左右のおもりの重さの比」が逆比になる
…といわれてもピンとこない方もいらっしゃるかもしれません。
難しい話はナシにして、基本2パターンを解説することでイメージを掴んでいただきましょう。
天秤法を扱える方は、この見出しを飛ばして一気に下の本題に進んでくださいね。
天秤法の例題1【長さから重さを導く】
天秤の支点から左6cmの点に50gのおもり、右4cmの点に( )gのおもりをつるすとつり合った。

「左右のうでの長さの比」が6cm:4cm=3:2となっています。
「左右のおもりの重さの比」は逆比で2:3。これを②g、③gと表しましょう。
②g=50gなので、③g=75gと求めることができましたね。
なお、このとき天秤は50g+75g=125gの力で下向きに引っ張られています。
これを支えるために支点は上向きに125gの力を天秤に加えていることになります。
「3:2だから2:3。おもりが75gで支点は125g!」
と暗算でできるようになれば完璧です。
それでは次の3問を暗算で解いてみましょう。
おもりの重さと支点にかかる力の両方を求めてみてくださいね。

正解は(1)おもり5gで支点15g、(2)おもり27gで支点45g、(3)おもり60gで支点105gです。
天秤法の例題2【重さから長さを導く】
天秤の支点から左3cmの点に30gのおもり、右( )cmの点に10gのおもりをつるすとつり合った。

「左右のおもりの重さの比」が30g:10g=3:1となっています。
「左右のうでの長さの比」は逆比で1:3。これを①cm、③cmと表しましょう。
①cm=3cmなので、③cm=9cmと求めることができましたね。
なお、このとき天秤は30g+10g=40gの力で下向きに引っ張られています。
これを支えるために支点は上向きに40gの力を天秤に加えていることになります。
「3:1だから1:3。長さが9cmで支点は40g!」
と暗算でできるようになれば完璧です。
それでは次の3問を暗算で解いてみましょう。
うでの長さと支点にかかる力の両方を求めてみてくださいね。

正解は(1)長さ3cmで支点90g、(2)長さ3cmで支点55g、(3)長さ13.3cmで支点39gです。
チェバの定理3パターン
それでは天秤法でチェバの定理を解く方法を伝授いたしましょう!
天秤法で解く際には交点LCM(最小公倍数)というポイントを用います。
チェバの定理1【外外パターン】
【外外パターン】とは、外の2辺の比が分かっている問題です。
図のような三角形ABCがあります。
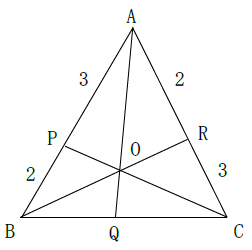
AP:PB=3:2、AR:RC=2:3であるとき、次の辺の比を求めよ。
(1)BQ:QC (2)AO:OQ (3)BO:OR (4)CO:OP
まずは辺AB、辺ACのそれぞれをうでの長さとする天秤があると考えます。
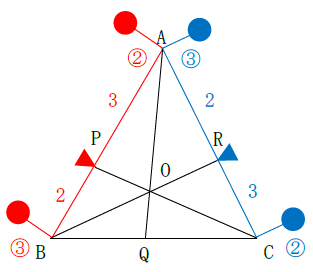
AP:PB=3:2なので、Aのおもり:Bのおもりは2g:3gとおけます。
AR:RC=2:3なので、Aのおもり:Cのおもりは3g:2gとおけます。
この2つの交点はAのおもりで、2gと3gのLCM(最小公倍数)6gにおきかえてみましょう。
すると、次のように重さを変えることができますね。
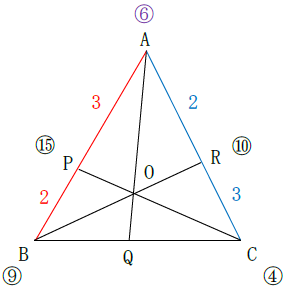
Bのおもりは9g、支点Pは6g+9g=15gとなります。
Cのおもりは4g、支点Rは6g+4g=10gとなります。
さて、辺AB、辺AC以外にも天秤がみえてきませんか?
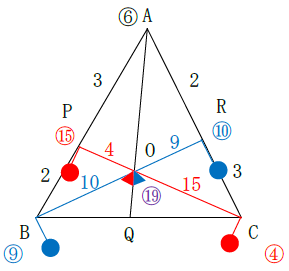
辺CPをうでの長さとする天秤に注目してみましょう。
Cのおもり:Pのおもり=4g:15gなのでCO:OP=15:4です。
辺BRをうでの長さとする天秤に注目してみましょう。
Bのおもり:Rのおもり=9g:10gなのでBO:OR=10:9です。
支点Oは4g+15g=9g+10g=19gと一致していますね。
同様に、辺BC、辺AQも天秤にしてみましょう。
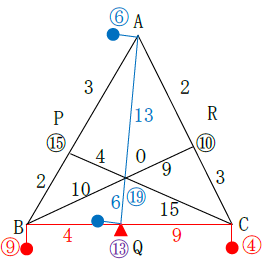
辺BCをうでの長さとする天秤に注目してみましょう。
Bのおもり:Cのおもり=9g:4gなのでBQ:QC=4:9です。
支点Qは9g+4g=13gとなります。
辺AQをうでの長さとする天秤に注目してみましょう。
Aのおもり:Qのおもり=6g:13gなのでAO:OQ=13:6です。
支点Oは6g+13g=19gとなり、これまでの支点Oと一致しますね。
正解は(1)4:9 (2)13:6 (3)10:9 (4)15:4となります。
一度紙に書いてトレーニングしてみましょう!
チェバの定理2【外内パターン】
次の三角形のように辺の比がわかっている場合でも、天秤法が同じように使えます。
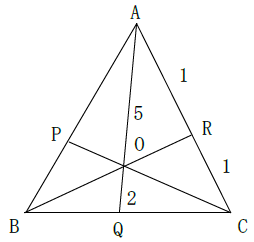
AR:RC=1:1、AO:OQ=5:2であるとき、次の辺の比を求めよ。
(1)AP:PB (2)BQ:QC (3)BO:OR (4)CO:OP
まずは辺AC、辺AQのそれぞれをうでの長さとする天秤があると考えます。
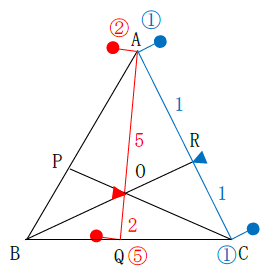
AR:RC=1:1なので、Aのおもり:Cのおもりは1g:1gとおけます。
AO:OQ=5:2なので、Aのおもり:Qのおもりは2g:5gとおけます。
この2つの交点はAのおもりで、1gと2gのLCM(最小公倍数)2gにおきかえてみましょう。
すると、次のように重さを変えることができますね。
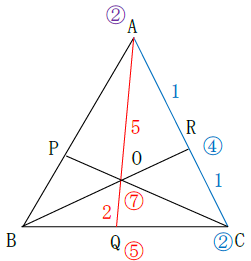
Cのおもりは2g、支点Rは2g+2g=4gとなります。
Qのおもりは5g、支点Oは2g+5g=7gとなります。
ここまでわかってしまえばこっちのもの!

Bのおもりは5g-2g=3gとなります。
Pのおもりは2g+3g=7g-2g=5gとなります。
後は同様に天秤法を用いましょう。
正解は(1)5:2 (2)2:3 (3)4:3 (4)5:2となります。
チェバの定理3【内内パターン】
チェバの問題で2辺の比がわかっていれば、天秤法がどんな時でも使えます。
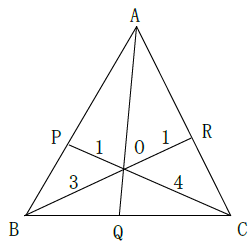
BO:OR=3:1、CO:OP=4:1であるとき、次の辺の比を求めよ。
(1)AP:PB (2)BQ:QC (3)CR:RA (4)AO:OQ
辺BRについて、Bのおもり1g、Rのおもり3g、支点O4gとします。
辺CPについて、Cのおもり1g、Pのおもり4g、支点O5gとします。
支点Oを4gと5gのLCM(最小公倍数)20gにおきかえてみましょう。
各点のおもりの重さは次のようになり、天秤法で答えが求められます。
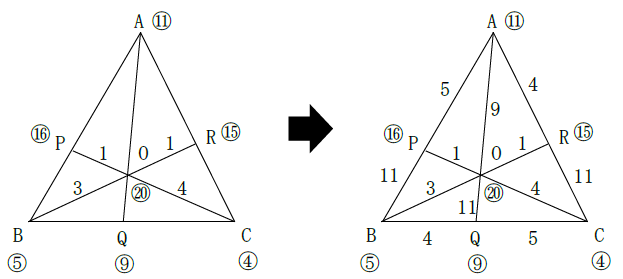
正解は(1)5:11 (2)4:5 (3)11:4 (4)9:11となります。
メネラウスの定理3パターン
メネラウスの定理も、チェバの定理と同じように天秤法で片づけてしまいましょう。
メネラウスの定理1【外外パターン】
次図において、AP:PB=4:5、BQ:QC=3:2であるとする。

次の辺の比を求めよ。
(1)AO:OQ (2)CO:OP
辺ABについて、Aのおもり5g、Bのおもり4g、支点P9gとします。
辺BCについて、Bのおもり2g、Cのおもり3g、支点Q5gとします。
Bのおもりを4gと2gのLCM(最小公倍数)4gにおきかえてみましょう。
各点のおもりの重さは次のようになり、天秤法で答えが求められます。
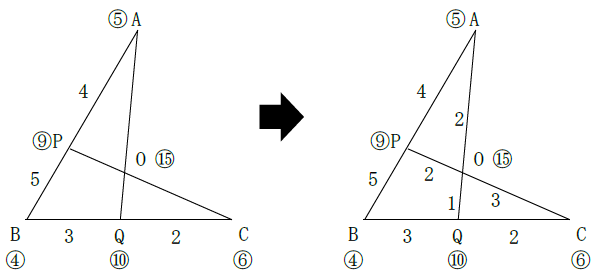
正解は(1)2:1 (2)3:2となります。
メネラウスの定理2【外内パターン】
次図において、AO:OQ=2:1、BQ:QC=3:1であるする。
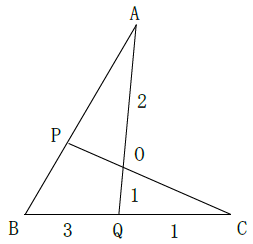
次の辺の比を求めよ。
(1)AP:PB (2)CO:OP
辺AQについて、Aのおもり1g、Qのおもり2g、支点O3gとします。
辺BCについて、Bのおもり1g、Cのおもり3g、支点Q4gとします。
Qのおもりを2gと4gのLCM(最小公倍数)4gにおきかえてみましょう。
各点のおもりの重さは次のようになり、天秤法で答えが求められます。
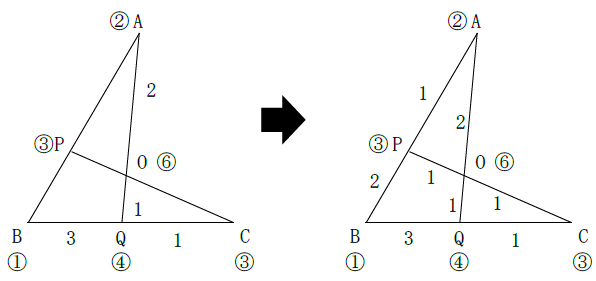
正解は(1)1:2 (2)1:1となります。
メネラウスの定理3【内内パターン】
次図において、AO:OQ=3:1、CO:OP=3:2であるとする。

次の辺の比を求めよ。
(1)AP:PB (2)BQ:QC
辺AQについて、Aのおもり1g、Qのおもり3g、支点O4gとします。
辺CPについて、Cのおもり2g、Pのおもり3g、支点O5gとします。
支点Oを4gと5gのLCM(最小公倍数)20gにおきかえてみましょう。
各点のおもりの重さは次のようになり、天秤法で答えが求められます。
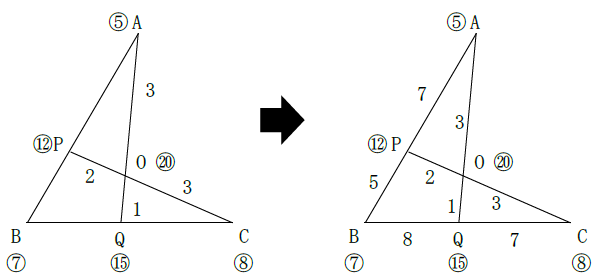
正解は(1)7:5 (2)8:7となります。
食塩濃度
ここからは食塩濃度の計算を天秤法で解く方法をご紹介いたしましょう。
天秤の長さ(cm)を濃さ(%)に置き換えて考えます。
食塩濃度1【二種混合パターン】
(1)7%の食塩水150gと15%の食塩水50gを混ぜると何%の食塩水になるか。
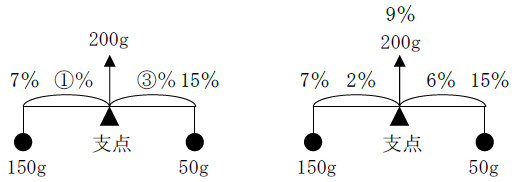
混ぜた二種類の食塩水をおもりとみなし、できた食塩水の位置を支点とみなします。
重さの比が150g:50g=3:1なので、長さ(濃さの差)の比は①%:③%となります。
①%+③%=④%=15%-7%=8%となることから、7%+2%=15%-6%=9%と求められます。
(2)100gの水に25gの食塩を溶かすと何%の食塩水になるか。

水を濃さ0%の食塩水とみなし、食塩を濃さ100%の食塩水とみなします。
重さの比が100g:25g=4:1なので、長さ(濃さの差)の比は①%:④%となります。
①%+④%=⑤%=100%となることから、0%+20%=100%-80%=20%となります。
食塩濃度2【水量増減パターン】
(1)濃さ18%の食塩水100gに水を加えて、3倍に薄めた。加えた水は何gか。

18%÷3=6%の濃さになることが分かります。
長さ(濃さの差)が6%:(18%-6%)=1:2なので、重さの比は②g:①gになります。
以上から100g×2=200gと求められます。
(2)濃さ4%の食塩水100gを加熱して水を一部蒸発させ、5倍の濃さにした。蒸発させた水は何gか。
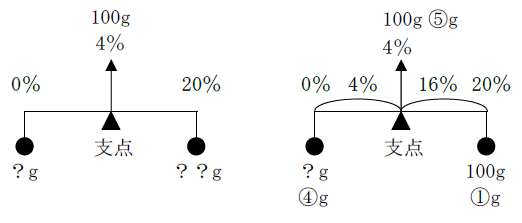
4%×5=20%の濃さになることが分かります。
長さ(濃さの差)の比が4%:(20%-4%)=1:4なので、重さの比は④g:①gになります。
以上から、100g÷5×4=80gと求められます。
食塩濃度3【等量交換パターン】
(1)濃さ7.5%の食塩水900gからxgの食塩水を取り出し、同じ重さの水を加えると濃さ5%になった。xに適する数値を求めよ。

残った7.5%の食塩水と水(0%の食塩水)を混ぜることで、総量は900gに戻ります。
長さ(濃さの差)の比が5%:(7.5%-5%)=2:1なので、重さの比は①g:②gになります。
以上から、900g÷3=300gと求められます。
シンプル・イズ・ザ・ベスト
いかがでしたか?
小学生でも学習して理解できるテクニックだからこそ、極めてシンプルに問題を解くことができるのです。
学年をまたいで技術を習得する心構えをもつ学生は、間違いなく柔軟で屈強に育つことでしょう。



コメントを残す